Though not essential an understanding of the underlying computer concepts and principles is useful. This may not seem directly relevant to modern programming in the beginning, but humor me. With that in mind, we are going to start a little closer to the bottom.
A lot of these concepts are simpler to explain if we go back to 8bit architecture. All modern computing is more or less based on these concepts just scale up to 64bits.
Programming Languages
There is one thing I’m going to point out, programming languages like C# are for human comprehension of code and not for the computer. These languages, called high-level languages because they are several thousand feet above the native language of the computer, arrived in the 1960s. In contrast, computers natively use machine code, a language made up of a relatively small set of instructions. These instructions are predefined in hardware and usually include binary operations and the movement of data between registers and/or address locations.
Data Structures
Within most 8bit architectures, “things” can be represented in either 8bits a byte, or 16bit (2 bytes) a word (words can be larger than 2 bytes on modern systems but for this introduction, we will be sticking to 16bit words for now). These two data types are the building blocks of anything you want. They can natively represent simple types like numbers and characters. The use of pointers and other concepts allows for more complex structures, but we will come to how those work a bit later on in this series.
Covering The Bases
There are some fundamental concepts in representing and converting binary to and from other native data types. We are going to start with numbers, unsigned integers to be specific. This is the first step in understanding binary.
Unsigned integers are positive whole numbers from 0 up.
To natively represent anything in a computer we use binary or base 2 this means there are only two digits 1 and 0 to represent numbers, whereas in base 10 (decimal) we use ten digits 0 to 9.
Using binary to count would look like this 0, 1, 10, 11, 100, 101, 110, 111. Compared to the same sequence in decimal 0, 1, 2, 3, 4, 5, 6, 7.
Binary 2 Decimal
Taking a byte from, left, Most Significant Bit (MSB) to, right, Least Significant Bit (LSB).
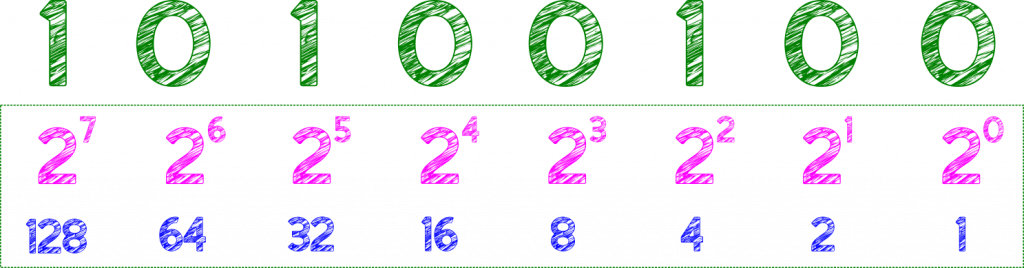
Each digit can be taken as a power of 2, to convert a binary number to decimal, add up the power values for the bits (digits) set to 1 in the above (10100100) 4 + 32 + 128 = 164
10 Types Of People
Hopefully, this brief introduction to base 2, explains the following T-Shirt slogan. “There are 10 types of people, those that understand binary and those that don’t!”
The Hexadecimal, Quaternary
Binary, though used in the computer everywhere, its written form in any language is rare. There are another two number bases, commonly used in computing, these are base 16 and base 4.
Base 16, commonly called Hexadecimal, uses 16 digits 0-F.
Base 4, or Quaternary, uses 4 digits 0-3.
Block Equivalence
The reason for their use hails from their relative ease of conversion to and from binary (again this is for our benefit, not the computers)
e.g.
Base 2 (Binary) – 11111111
Base 4 (Quaternary) – 3333
Base 16 (Hexadecimal) – FF
In our native culture base 10 (Decimal) this is 255
The decimal math below illustrates the conversion, of the above, from base 4 by breaking down the conversion of each digit (left to right)
3 x 4 x 4 x 4 (3000 in quaternary, 192 in decimal) +
3 x 4 x 4 (300 in quaternary, 48 in decimal ) +
3 x 4 (30 in quaternary, 12 in decimal ) +
3 (3 in quaternary, 3 in decimal )
So in base 4 “10” is 4 so multiplying by 4 is like multiplying by 10 in decimal, it adds a 0
So we can see that the above digit conversions add up as expected, 192 + 48 + 12 + 3 = 255
Conversion from binary to bases 4 and 16 is logical, because there is a block equivalence in base 4 and 16
4 digits in base 2 represent 2 digits in base 4
8 digits (bits) in base 2 (a byte) represents 2 digits in base 16
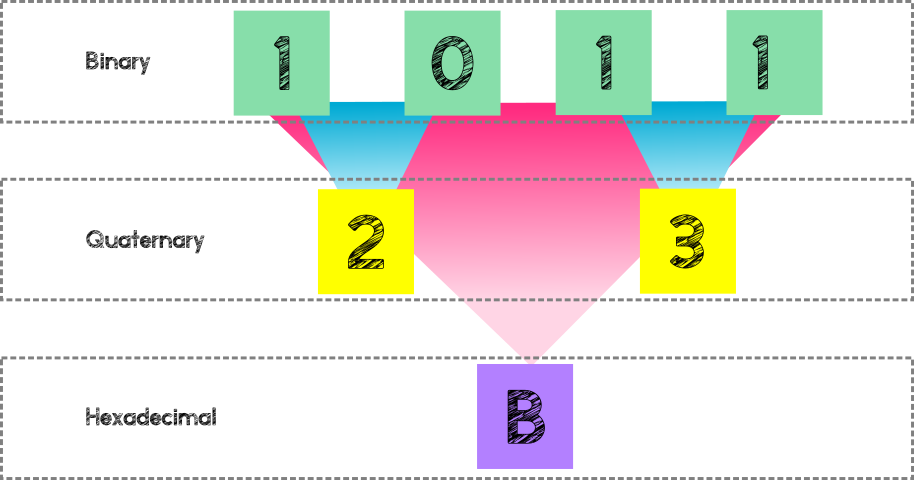
Base 4, though rarely used today is still useful to illustrate this conversion concept and did have merits in older architectures.
Why Not Go Big?
Base 256 would be the next logical step for 1 digit per 8 bits (byte). However, because the aim is to make this simpler for us to read and understand this falls down due to the lack of an existing symbolic system to support this number of unique digits.
So the sweet spot is hexadecimal, and you will see this used throughout computing and coding alike.
Programming Part I Round-Up
In this first part of “Programming” from the beginning, we have covered why the use of hexadecimal became prevalent in computing and how we represent unsigned integers in Base 2, 4 and 16. We have also covered a method for converting Binary to Decimal and the binary block equivalence that exists in base 4 and 16.
But what about negative numbers, boolean, fractions, decimal and characters, and other more complex structures?
Well that will be in Part II



