If you missed part one then you can catch up here
Two’s a Complement?
Signed integers, the first order of business, if you recall we covered simple unsigned integers in Part I. The most common method for representing signed integers in binary is twos complement. I have found the simplest way to look at this is taking the most significant bit and treating that as the same magnitude but negative.
In 8bits that makes the MSB -128. Then add the remaining bit values as before. In 8 bits this gives a range of -128 to 127 so for this to be useful we need at least 16 bits to give -32,768 to 32,767
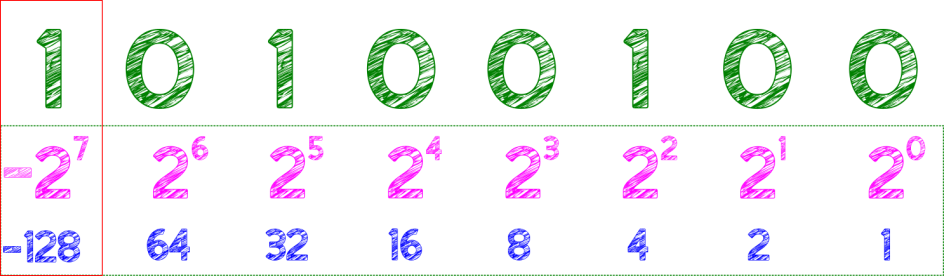
bool(eans) -1 or Not -1
This leads to another, not so obviously linked, data type bool or boolean i.e. true or false.
Boolean’s are usually represented by a byte or word, even though logically a bit would do. A byte or word gets used because these are the smallest logical addressable block. So really nothing is to be gained by using a single bit.
In C and some other languages, you will sometimes see -1 used in place of true, this doesn’t seem to make sense until you consider how a byte with all bits set would be interpreted using two complements. 11111111 is -1 and 00000000 is 0 so all 1s true all zeros false (some languages consider -1 as true and anything else as false)
Interestingly this is true regardless of the data width 1, 4, 8, 16, 32, 64 or 128 bits, when all bits are set to 1 the decimal value is -1, and yes this still works with 1 bit as 1 bit in twos-complement has a range of -1 to 0
This makes -1 a bit width agnostic representation of true when using twos complement.
Fractions
Fractions come in two types the accurate and approximate the latter is more space-efficient which in the early days of computer hardware was a necessary evil.
But this approximate method is still very much alive today in the form of float/single and double data types.
History
This concept is an exception that does not follow the 8bit scale up the concept. Most 8-bit floating-point implementations were outside of hardware and proprietary. Most floating-point implementations, in the 8-bit world, were software or firmware.
Math Co-Processors
The 16-bit world introduced the concept of a math co-processor, which included a Floating Point Unit (FPU). The FPU allowed hardware-accelerated math operations including those on floating-point numbers. Intel’s complemented its 8086 with an 8087 math co-processor. Floating-point operations were possible without the 8087, but this used software implementations similar to the 8bit world that came before.
This period also introduced Intel’s iterative 8088 which was, confusingly, a “cut-down” version of the 8086 with an 8bit address bus to allow the use of cheaper (and slower) supporting chips for the emerging home computer market. The 8088 processor was also capable of utilising the 8087 like its big brother the 8086, though rarely paired in production hardware.
The math coprocessor in the intel x86 range maintained its 87 designations throughout the range 80187, 80287, 80387 and ended with the 80487 which was actually an 80486SX with an integrated math co-processor, the 80486DX had the same integrated architecture but with a different chip pinout.
From this point on floating-point operations, certainly for intel, are now part of the processor native capability.
Common Implementation
In most implementations of a floating-point there are 2 types called single and double these use the same method but are differing binary widths, single usually being 32bit and double being 64bit. The single and double refers to the precision the bit width provides.
Taking the single, for example, the 32bits consists of three elements the sign, the mantissa and the exponent. Similar to decimal floating-point notation e.g. +1.326e5.
Reading from the MSB to the LSB, 1 bit used as the sign, followed by 8 bits as the exponent and 23 bits as the mantissa.

The mantissa, normalised to 1 set bit before the point and 23-bit places. We can, therefore, drop the one before the point for storage, only storing the remaining 23-bits after the point.
Binary fractions
| Binary | Power | Decimal Fraction | Decimal Value |
|---|---|---|---|
| 0.1 | 1/2 1 | 1/2 | 0.5 |
| 0.01 | 1/2 2 | 1/4 | 0.25 |
| 0.001 | 1/2 3 | 1/8 | 0.125 |
| 0.0001 | 1/2 4 | 1/16 | 0.0625 |
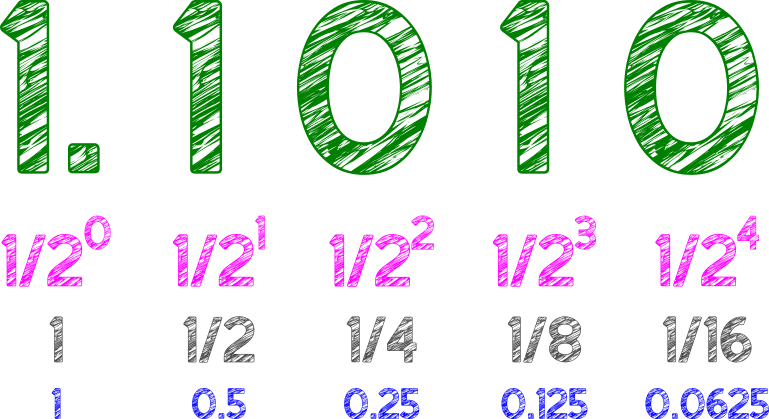
Example the decimal equivalent of 1.101 is
1 + 1/2 + 1/8
1 + 0.5 + 0.125
=1.625 in decimal
The errors, or inaccuracies, mentioned above, arise from the limitations of binary fractions and their storage in this floating-point notation.
Exponent
The exponent is also binary and if we used twos-complement that would look something like this
0 11111101 10110100000000000000000
Using signed binary exponent notation
+1.101101e-11
Expands to
+1101.101
=13.625 in decimal
Exponent Bias
… But… It’s not quite as simple as that because of a need to represent three special states, 0, infinity and NaN (Not a Number) the common convention is to represent the exponent as an unsigned number by using an “exponent bias” of 127
If you consider the lowest number possible with 8-bit 2s complement is -128 anyway the net result of the 127 bias is that all 0s is -127 and all 1s is 255-127 128
So what’s stored in the exponent +127 and to calculate we have to take the stored value and take the 127 off giving the true exponent value.
Making our exponent in the above -3 + 127 =124
0 01111100 10110100000000000000000
Zero, Infinity and NaN
However, to cover the special cases we take the following binary states into account.
With all bits of the exponent field set to 0, the floating-point number is considered to be 0.0
0 00000000 10110100000000000000000
The fraction and sign elements are ignored.
With all bits of the exponent field set to 1 and the fraction part as 0, then the floating-point number is considered to be infinity.
0 11111111 00000000000000000000000
Finally, with all bits of the exponent field set to 1 but the fraction part set to a non zero value, the floating-point number is considered in a NaN state.
0 11111111 10110100000000000000000
A fraction can be anything EXCEPT all 0s
That was a bigger journey than I expected so we will cover the decimal type, binary coded decimal, characters and stings to follow in Part III.